In physics, there is zero distinction between past, present, and future besides the meaning we humans ascribe to it.
“To those of us who believe in physics,” he wrote in 1955 to the family of a friend who had recently died, “
this separation between past, present, and future is only an illusion, if a stubborn one.” When his own turn came, a few weeks later, Einstein said, “It is time to go.”
This demonstrates that there is no clear distinction between past, present and future, but that they all coexist in spacetime. The events that we consider in the past or future are equally real, it is only our limited perspective that makes us perceive time as a linear flow.
This interesting video by Brian Greene clearly and accessibly explains Einstein’s theory of relativity and how it radically changes our…

medium.com
Unlike Gödel, Einstein could never quite liberate himself from the grip of time. “To those of us who believe in physics,” he wrote in 1955 to the family of a friend who had recently died, “this separation between past, present, and future is only an illusion, if a stubborn one.” When his own turn came, a few weeks later, Einstein said, “It is time to go.”
In short, according to the theory of relativity time does not flow in an absolute way, but depends on the inertial frame of reference of the observer. Past, present and future all coexist in spacetime and are interconnected, there is no clear distinction between them. This radically new conception of time is demonstrated by experiments on time dilation.
If you don't believe me then you can (and should) read up on the works of
Douglas Hofstadter. Here, I'll quote the
Wiki page:
By exploring common themes in the lives and works of logician
Kurt Gödel, artist
M. C. Escher, and composer
Johann Sebastian Bach, the book expounds concepts fundamental to
mathematics,
symmetry, and
intelligence. Through short stories, illustrations, and analysis, the book discusses how systems can acquire meaningful context despite being made of "meaningless" elements. It also discusses
self-reference and formal rules,
isomorphism, what it means to communicate, how knowledge can be represented and stored, the methods and limitations of symbolic representation, and even the fundamental notion of "meaning" itself.
In response to confusion over the book's theme, Hofstadter emphasized that
Gödel, Escher, Bach is not about the relationships of
mathematics, art, and
music, but rather about how
cognition emerges from hidden neurological mechanisms. One point in the book presents an analogy about how individual
neurons in the
brain coordinate to create a unified sense of a coherent mind by comparing it to the social organization displayed in a
colony of ants.
You may also like:
But I think you should definitely read the works of Roy Herbert
Here's a video on his theory of his Dilation Theory.
You said we exist in a universe that has 3 Dimensions.
Now, what if I told you that there could be, and probably definitely are, infinite other higher dimensions that one who only knows, understands, lives in, and whose whole belief system is based inside of the third dimension?
What if I told you that there is no dimension of time because time is a construct of an intelligent living organism that is experienced by its consciousness when 2 main factors are at play?
The 2 main factors at play here are:
1. Gravity
2. Density
This is why time dilation exists.
You should go (re)watch "Interstellar". It explains time dilation pretty well by the end of the movie.
Edit: Regarding your 10 Dimension theory:
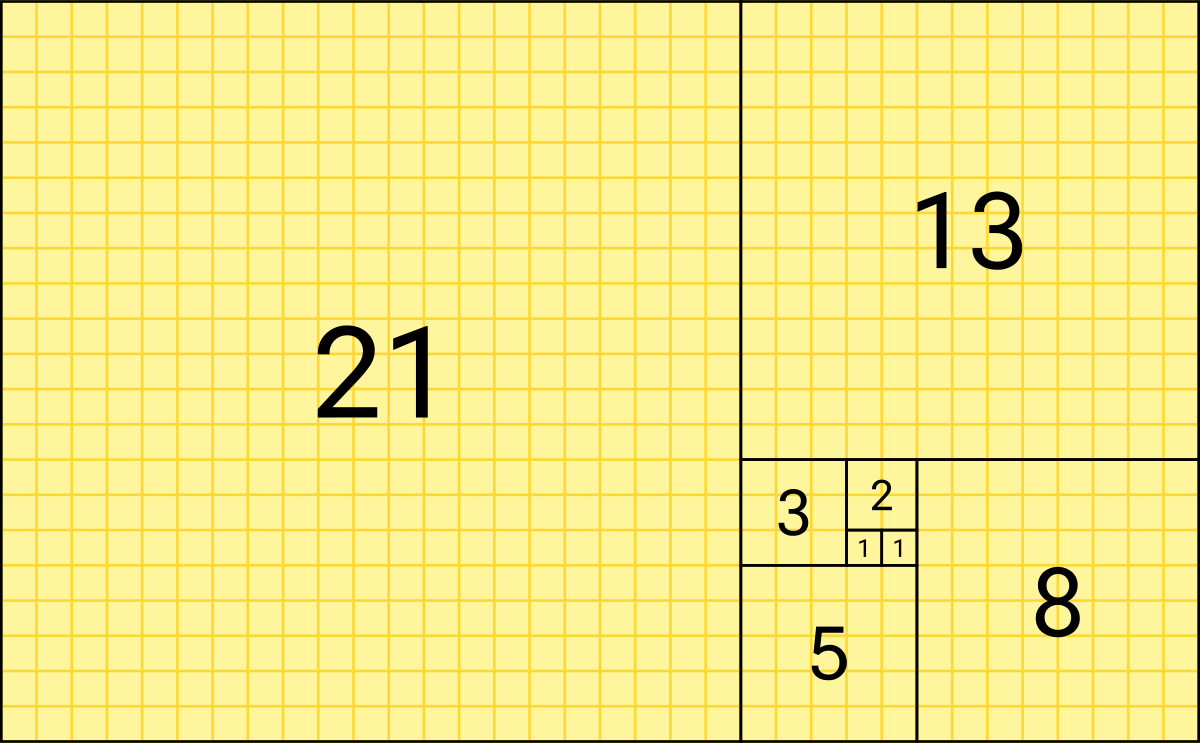
It sounds as if you are referring to the Fibonacci Sequence.

en.wikipedia.org
In mathematics, the
Fibonacci sequence is a
sequence in which each term is the sum of the two terms that precede it. Numbers that are part of the Fibonacci sequence are known as
Fibonacci numbers, commonly denoted
Fn. Many writers begin the sequence with 0 and 1, although some authors start it from 1 and 1 from 1 and 2. Starting from 0 and 1, the sequence begins
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... (sequence
A000045 in the
OEIS)
You may or may not have heard of this, and that's okay.
But the Fibonacci Sequence is important based on how it is graphed, as it is a series of patterns found everwhere in nature
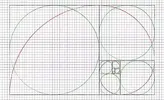

The golden ratio can be found in nature in various forms, including the spiral patterns of snail shells, nautilus shells, pinecones, sunflower seed heads, and the arrangement of leaves on a stem, where the ratio between successive segments often approximates the golden ratio (approximately 1.618).
This is even true for your fingerprints. The Golden Spiral is everywhere in nature.
1.61803399 is the value associated with "Phi".
The golden ratio, also known as the golden number, golden proportion, or the divine proportion, is a ratio between two numbers that equals approximately 1.618. Usually written as the Greek letter phi, it is strongly associated with the Fibonacci sequence, a series of numbers wherein each number is added to the last. The Fibonacci numbers are 0, 1, 1, 2, 3, 5, 8, 13, 21, and so on, with the ratio of each number and the previous number gradually approaching 1.618, or phi.
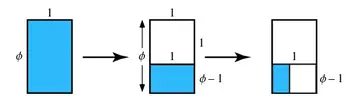
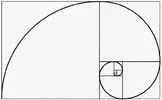
As you can see in the middle panel above, a large Golden Rectangle can be subdivided into a smaller Golden Rectangle, rotated 90 degrees (blue), and a square (white). You can continue this process as long as you like, making a figure full of nothing but golden rectangles and squares at different scales.
If you keep filling in the Golden Rectangle by scaling and rotating copies of itself, you can observe a logarithmic spiral emerge:
Again, this is a pattern that appears everywhere in nature.
It's prevalent in a movie by the name "Pi". Mathematically Phi is just 1/2 of Pi, in mathematical representation, and they are both irrational numbers, or decimal numbers that do not end.
Sources:
The golden ration is one of the most famous ratios in mathematics and design. Learn more about the golden ratio and its role in art and design.
www.adobe.com

en.wikipedia.org
Answer (1 of 23): Consider 2 numbers A and B. Let us take B>=A A and B are said to be in golden ratio, if \frac{A+B}{B} = \frac{B}{A} The Golden Ratio is a constant and is represented by the symbol \phi or 'Phi'. This is how I derived of the value of Phi. We have \frac{A+B}{B} = \frac{B}{A} ...

www.quora.com